2020년도 대한민국 국제정보올림피아드 선발고사 풀이 (Day 1)

 

 

 

그날의 복수를 하러 왔다

 

선발고사에서 떨어진 아픈 기억이 있는 셋이다.(스코어보드상 6등)

과거의 상처를 극복하고 싶어서 2월 1일 13시 30분에 시작하는 셋을 만들었고, 2월 3일 7시 52분에 대회장에서 풀지 못했던 마지막 문제인 지름길을, 9시 6분에 마법의 다이얼과 칠하기를 다시 구현하기를 끝내며 모든 문제를 BOJ에서 AC를 받았다.

인터넷을 찾아보니 정휘님 블로그 글이 있긴 한데, 다른 블로그와 중복된 자료를 싫어하는 편이지만 세 문제의 풀이가 빠져 있어 작성한다.

 

 

Day 1

 

 

1. 문자열 찾기(BOJ 25008)

 

Solution

 

P에 대해서 '사실상 같은' 실패함수를 만들어줄 수 있다. $i$번째로 등장하는 문자가 $fail(i)$가 커버하는 범위에서 이미 등장한 적 있다면, 해당 문자와 같은 문자로 생각하여 비교한다. 각 알파벳 소문자에 대하여, 해당 문자가 직전에 나온 위치인 $prev(c)$를 관리한다면 쉽게 관리가 가능하다.

실패함수를 만들었다면, 같은 방법으로 KMP 본 과정도 구현할 수 있다.

 

시간복잡도는 $O(N+M)$.

 

Code : http://boj.kr/a9d9effdefa141efa6302479fff09849

 

여담.

2020년도 선발고사에 이 문제가 출제되고, 2021년도 SCPC 2차 예선에 이 문제를 KMP 대신 아호코라식으로 구현해야 하는 "패턴 매칭"이라는 문제가 출제되었다. 다시 구현하기 귀찮아서 패턴 매칭 문제의 코드를 그대로 갖다가 제출했다.

 

 

2. 뚫기(BOJ 25009)

 

Subtask #1, 2(29점)

 

각 쿼리가 들어올 때마다 문제를 풀어주자.

다음의 쿼리들을 수행할 수 있는 세그먼트 트리를 만들어줄 수 있다.

• $a[i] := min(a[i], v)$ ($\forall i \in [l, r]$)
• $a[i] := a[i] + v$ ($\forall i \in [l, r]$)

 

오른쪽으로 한 칸 이동하는 것은 막이 존재하는 위치에 대해서 뚫기를, 위아래로 움직이는 것은 전체 위치 중 가장 현재까지의 비용이 낮은 위치에서부터 이동한다고 생각할 수 있다. 따라서 한번의 minimize 쿼리를 $O(NlogN)$에 처리할 수 있다.

$M$의 범위가 큰 것은 좌표압축을 통해서 $O(N)$개의 위치만 남길 수 있다.

 

시간복잡도는 $O(QNlogN)$.

 

Subtask #3(48점)

 

$x=0$에서 $x=N$까지 이동할 때 가능한 모든 경로에 대해 (순간이동 횟수, 뚫기 횟수)쌍을 구했다고 가정하자.

1. 각각의 횟수는 $N$을 넘지 않고($(0, 0)$ ~ $(N, N)$)
2. $x_i \leq x_j$, $y_i \leq y_j$인 $(x_i, y_i)$와 $(x_j, y_j)$가 있다면 $(x_j, y_j)$는 사용할 이유가 없고($x$가 증가함에 따라 $y$는 단조감소)
3. $A = y$, $B = x$에 대해서 문제를 풀었을 때 각각의 횟수가 $(x, y)$가 나온다면 해당 순서쌍은 이동 방법으로 가능하며 자신보다 상위호환인 순서쌍이 존재하지 않는, 소위 '의미 있는' 순서쌍이다.

 

가능한 모든 $(x, y)$에 대하여 $A=y, B=x$로 문제를 풀어, 의미 있는 순서쌍을 전부 모아보자.

한 번 문제를 푸는데 $(NlogN)$가 걸리기 때문에 의미 있는 순서쌍을 모두 모으는 데에는 $O(N^3logN)$의 시간이 걸린다.

의미 있는 순서쌍의 개수는 $O(N)$개가 나올 것이며, 각 쿼리마다 모든 순서쌍을 한번씩 확인하여 최적인 값을 직접 찾아주면 된다.

 

시간복잡도는 $O(N^3logN + NQ)$.

 

Full Solution(100점)

 

의미 있는 순서쌍들은 Convex Hull을 이룬다. A와 B가 주어졌을 때, 비용이 가능한 모든 $B(xA/B+y)$ 중 최솟값이며, 이를 B로 나눠보면 기울기가 $x$, $y$절편이 $y$인 일차함수들의 $x = A/B$에서의 최솟값이라고 생각할 수 있다. 따라서, 그래프를 생각해보면 Concave하며, 이는 의미 있는 순서쌍들이 Convex Hull을 이룬다는 뜻이기도 하다.

 

어떤 기울기에 대한 Convex Hull에서의 접점을 빠르게 구할 수 있다. 기울기 $-x/y$에 대하여, $A = y$, $B = x$로 문제를 풀면 나오는 순서쌍이 Convex Hull에서의 접점이다($(x, y)$ 순서쌍은 $x$회 순간이동, $y$회 뚫기를 했다는 뜻인데, 그러면 순간이동에 $y$, 뚫기에 $x$의 코스트를 매기면 $x$회 순간이동과 $y$회 뚫기의 가치가 같아진다.).

 

좌표범위가 $[0, N]$이기 때문에, Convex Hull 상의 점의 개수는 $O(N^{2/3})$개이다. 모든 의미 있는 순서쌍을 구해주고, 각 minimize 쿼리마다 이분 탐색을 통해(사실 순서쌍의 개수가 많지 않아 모든 순서쌍을 확인해주어도 AC가 나온다.) 최적인 값을 찾아줄 수 있다.

 

시간복잡도는 $O(N^{5/3}logN + QlogN)$, 또는 $O(N^{5/3}logN + QN^{2/3})$.

 

Code : http://boj.kr/fe952fed1b3f49c092fe19bd278866a0

 

 

3. 지름길(BOJ 25010)

 

Subtask #5(87점)

 

파라매트릭 서치로, 답으로 K 이하의 수가 가능한지를 판별하는 결정 문제로 바꾼다.

$l$ - $r$ 사이의 지름길을 만든다고 생각하자.

지름길이 없을 때 $0$번 정점에서 $i$번 정점까지의 거리를 $P_i$라고 정의한다.

생각해야하는 조건은 $P_j - P_i > K$인 모든 $(i, j)$ 순서쌍에 대하여, $|P_l - P_i| + |P_r - P_j| + dist(l, r) \leq K$ 부등식을 만족해야 한다.

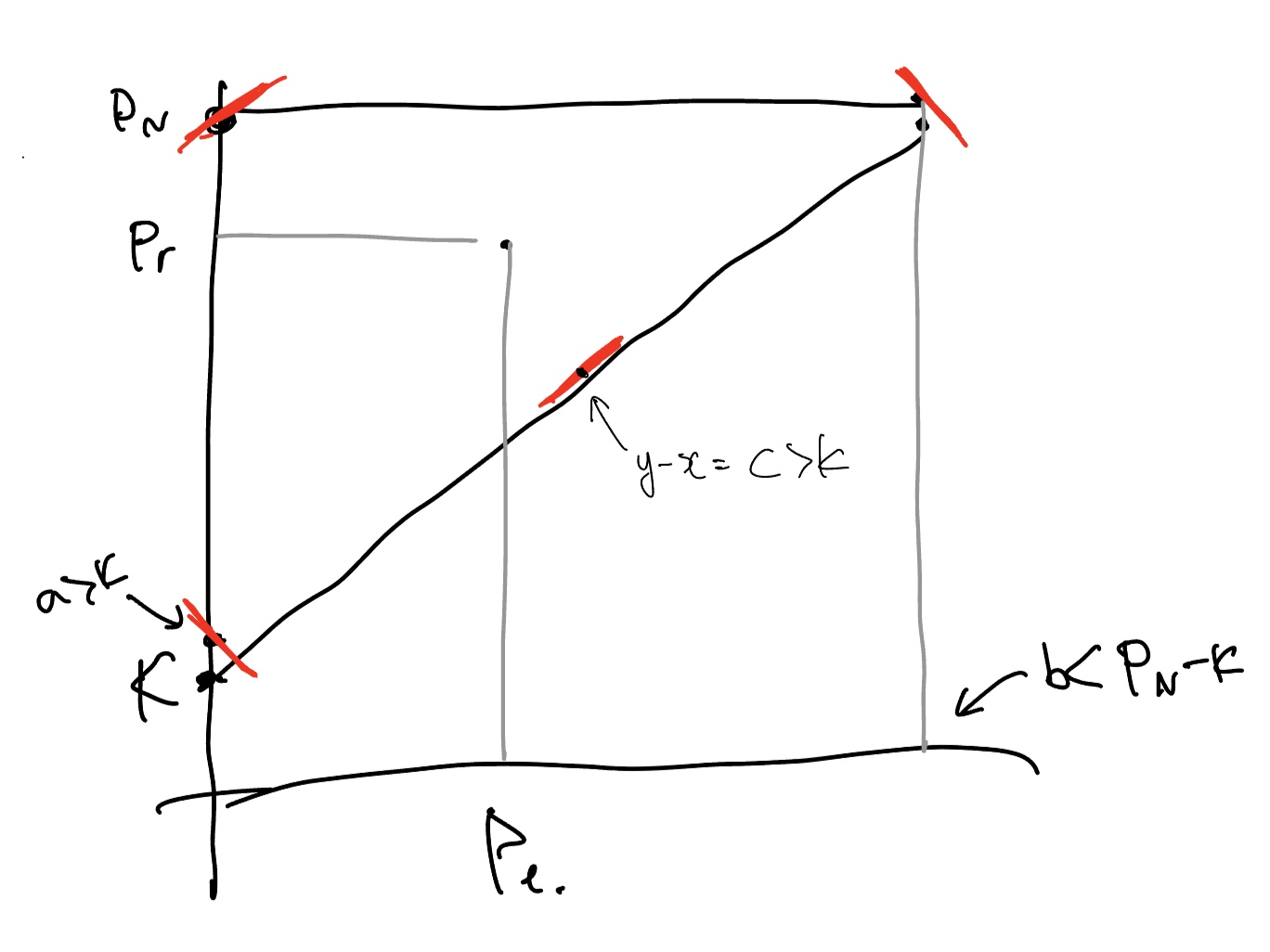
좌표평면에 그림과 같이 $(P_i, P_j)$들을 표시해 보면, 각 $i$에 대하여 최소와 최대의 $j$만 확인하면 된다. 최소의 $j$는 $P$에서의 $(P_i + K)$의 upper bound이며, 최대의 $j$는 $N$이다.

이 중에서도 특히 확인해야 하는 점은 총 4개밖에 없다. $(0, a(>K))$, $(0, P_{N-1})$, $(P_i, P_i + c(>K))$, $(b, P_{N-1})$이다. 각각 가능한 값들 중에 $a$는 최솟값, $b$는 최댓값, $c$는 최솟값이다.

 

부등식을 정리해보면

• $P_r + dist(l, r) \leq min(K + a - P_l, K + c + P_l)$
• $P_r - dist(l, r) \geq max(P_{N-1} - K + P_l, b + P_{N-1} - K - P_l)$

 

이 나온다. 사실 그렇게 엄밀한 부등식은 아니지만, 저 부등식이 오류가 나는 구역을 생각해 보면 어차피 답이 존재하지 않는다는 것을 알 수 있다.

 

일반성을 잃지 않고 $x_l \leq x_r$, $y_l \leq y_r$이라고 가정하면, $(P_r + x_r + y_r)$의 상한과 $(P_r - x_r - y_r)$의 하한이 결정된다. 따라서, 이차원 평면에서 $x$가 감소하는 방향으로 스위핑하며, 현재 정점을 $l$로 두고 문제를 풀면 된다. 지금까지 추가된 정점 중 $y$좌표가 현재 정점보다 작지 않고, 위의 부등식을 만족하는 점이 존재하는지를 확인하면 된다. $l \leq r$ 조건은 무시해도 상관없다.

 

$a_r = (P_r + x_r + y_r)$, $b_r = (P_r - x_r - y_r)$이라고 가정하자. $a_r$은 작은 것이, $b_r$은 큰 것이 이득이기 때문에 단조성을 띄게 deque로 관리할 수 있다. 세그먼트 트리의 각 노드에서 deque를 관리하면 정점 추가에 amortized $O(logN)$, 조건 확인에 이분 탐색을 이용하여 $O(log^2N)$의 시간이 걸린다.

$x_l \leq x_r$, $y_l \leq y_r$라고 가정하였기 때문에 모든 $(l, r)$을 확인하려면 좌표평면을 90도씩 회전시키며 같은 과정을 네 번 반복하면 된다.

 

총 시간복잡도는 $O(Nlog^2NlogX)$.

 

Full Solution(100점)

 

위의 풀이는 치워두고, 식 정리가 아닌 관찰로 얻을 수 있는 사실들을 나열해 보자.

1. $0$ - $l$ - $r$ - $r_0$($K < r_0 \leq r$) : $l$이 감소할수록, 가능한 최대 $r$은 증가한다.
2. $0$ - $l$ - $r$ - $(N-1)$ : $l$이 증가할수록, 가능한 최소 $r$은 증가한다.
3. $i$ - $l$ - $r$ - $j$($l < i$, $j < r$, $P_j - P_i > K$) : $l$이 증가할수록, 가능한 최대 $r$은 증가한다.
4. $l_{N-1}$ - $l$ - $r$ - $(N-1)$($l_{N-1} < P_{N-1} - K$, $l < l_{N-1}$) : $r$이 증가할수록, 가능한 최소 $l$은 감소한다.

 

위는 전부 삼각부등식으로 증명할 수 있다. 유클리드 거리가 아닌 택시 거리이지만, 삼각부등식이 성립한다.

 

1, 2, 4는 투포인터로, 3은 거기에 추가적으로 $[l, r]$ 구간 내에 있는 $(i, j)$($P_j - P_i > K$) 순서쌍에 대해서 $(P_j - P_i)$의 최솟값을 deque으로 관리하여 해결할 수 있다.

 

네 가지 조건을 계산하는데 $O(N)$, 네 가지 조건을 모두 만족하는 $(l, r)$ 쌍이 존재하는지 $O(N)$에 처리가 가능하므로, 결정 문제를 $O(N)$에 풀 수 있다.

 

따라서 시간복잡도는 $O(NlogX)$.

 

Code : http://boj.kr/3695a91850de48779e0bd3e69d2b2999

 

 

4. 칠하기(BOJ 25011)

 

Solution

 

가로로 연속한 이동 가능한 칸들을 하나의 정점으로, 세로로 연속한 이동 가능한 칸들을 하나의 정점으로 묶을 수 있다. 벽 또는 이동 불가능한 칸에 부딪히는 경우, 해당 칸을 이용하여 간선을 연결시킬 수 있다.

이제 평범한 방향 그래프가 생겼고, 원래의 문제는 '어떤 정점에서부터 시작해서 모든 정점을 순회할 수 있는가'라는 문제로 바뀌었다. 정점들을 SCC로 묶고, SCC끼리 위상정렬을 하고, 위상정렬 순서를 보면서 한 SCC에서 다음 SCC로 넘어가는 간선이 존재하는지를 확인하면 문제를 해결할 수 있다. 만약 존재하지 않는다면, 구하고자 하는 순회 방법이 존재하지 않는다. 

 

시간복잡도는 $O(NM)$.

 

Code : http://boj.kr/b284a8a30bc74957924d2893d6c749d9

 

여담.

구현하기가 너무 막막해서, 평소에도 즐겨 사용하는 atcoder library를 사용하여 SCC 구현을 처리했다. 실전에서는 못 쓰겠지만, 연습이니깐... 그리고 어차피 OI는 졸업했으니깐...

 

 

 

글을 작성하다가 너무 길어져서, Day 1과 Day 2로 분리합니다.